Java Collection Framework

Definition of wiki : The Java collections framework (JCF) is a set of classes and interfaces that implement commonly reusable collection data structures.

The above diagram contains the common implementation of collection framework

The above diagram contains the common implementation of Map.

Summary of Collection and Map Implementations

Concrete Collection/Map	Interface	Duplicates	Ordered/Sorted	Methods That Can Be Called On Elements	Data Structures on Which Implementation Is Based
HashSet<E>	Set<E>	Unique elements	No order	equals() hashCode()	Hash table and linked list
LinkedHashSet<E>	Set<E>	Unique elements	Insertion order	equals() hashCode()	Hash table and doubly-linked list
TreeSet<E>	Sorted-Set<E> NavigableSet<E>	Unique elements	Sorted	compareTo()	Balanced tree
ArrayList<E>	List<E>	Allowed	Insertion order	equals()	Resizable array
LinkedList<E >	List<E> Queue<E> Deque<E>	Allowed	Insertion/priority/deque order	equals() compareTo()	Linked list
Vector<E>	List<E>	Allowed	Insertion order	equals()	Resizable array
PriorityQueue<E>	Queue<E>	Allowed	Access according to priority order	compareTo()	Priority heap (tree-like structure)
ArrayDeque<E>	Queue<E> Deque<E>	Allowed	Access according to either FIFO or LIFO processing order	equals()	Resizable array
HashMap<K,v>	Map<K,V>	Unique keys	No order	equals() hashCode()	Hash table using array
LinkedHashMap<K,V>	Map<K,V>	Unique keys	Key insertion order/Access order of entries	equals() hashCode()	Hash table and doubly-linked list
Hashtable<K,V>	Map<K,V>	Unique keys	No order	equals() hashCode()	Hash table
TreeMap<K,V>	Sorted-Map<K,V> NavigableMap<K,V>	Unique keys	Sorted in key order	equals() compareTo()	Balanced tree

List Interface.
An ordered collection.

• The user of this interface has precise control over where in the list each element is inserted.
• The user can access elements by their integer index (position in the list), and search for elements in the list.

Interface provide contract for various methods like

1. Search for a specified object
2. Remove and insert elements at an arbitrary point in the list.

Key implementations of List interface

1. ArrayList<E>: A list implementation with underlying data structure is arrays.

1. Implements all optional list operations,
2. permits all elements, including null.
3. The size, isEmpty, get, set, iterator, and listIterator operations run in constant time.
4. Adding n elements requires O(n) time. An application can increase the capacity of an ArrayList instance before adding a large number of elements using the ensureCapacity operation. In ensureCapacity operation. if additional element increases the old capacity of array list then. Arrays are copied into new ArrayList with size = (oldCapacity * 3)/2 + 1

Key operations algorithm
1. Add (E e): Increase capacity if required and then add the element at the last in a new Array
2. Add(int index, E e) : Increase the capacity if required , then use System.arrayCopy to copy except the index postion
3. Remove(int index)  : use System.arrayCopy to shifts any subsequent elements to the left
4.  Remove(E e) : iterates over the array and removes the first element that matches in the array.

ArrayList provides random access and is more efficient at accessing elements but is generally slower at inserting and deleting elements.

2. LinkedList<E>: A doubly linked list implementation.

1. Implements all optional list operations,
2. permits all elements, including null.
3. The size, isEmpty, get, set, iterator, and listIterator operations run in constant time.
4. Insert operation is fast as you just have to change the pointers of the linked list instead of copying the whole array.
5. This data structure to be used when we frequently add and remove elements from the list.

Key operations algorithm
1. get(index) : Iterates over the list to get element.
2. Add (E e): Append the element at the end of the list
3. Add(int index, E e) : get the element at the index position and then set the object at that index
4. Remove(int index)  : get the element at the index position and then set remove the object references.
5.  Remove(E e) : Removes the first occurrence of the specified element from the list.

LinkedList provides sequential access and is generally more efficient at inserting and deleting elements in the list, however, it is it less efficient at accessing elements in a list.

Map<K,V> Interface. 

An object that maps keys to values. A map cannot contain duplicate keys; each key can map to at most one value. 

Interface provide contract for various methods like

1. Search for a specified object based on key
2. Get and put elements based on keys.

Key implementations of Map interface

1. HashMap<K,V>: A map implementation with underlying data structure a array of linked lists.

1. Implements all optional map operations,
2. permits key and value as null.
3. This implementation provides constant-time performance for the basic operations (get and put),.
4. An instance of HashMap has two parameters that affect its performance: initial capacity and load factor. The capacity is the number of buckets in the hash table, and the initial capacity is simply the capacity at the time the hash table is created. The load factor is a measure of how full the hash table is allowed to get before its capacity is automatically increased. When the number of entries in the hash table exceeds the product of the load factor and the current capacity, the hash table is rehashed (that is, internal data structures are rebuilt) so that the hash table has approximately twice the number of buckets. 
5.  threshold is DEFAULT_INITIAL_CAPACITY * DEFAULT_LOAD_FACTOR

Key operations algorithm
1. get (k key):

•  hash the key : int hash = hash(key.hashCode());
•  get the index of linked list array based on hash key and table length
• Iterate over the linked list at that index till key with same reference or equal value is not found

2. put (k key,V value):

•  hash the key : int hash = hash(key.hashCode());
•  get the index of linked list array based on hash key and table length
• Iterate over the linked list at that index till key with same reference or equal value is not found and replace the old value
• If the key does not exist then create a new entry at index calculated in step 2 and then re-size the table of linked list

 
     
HashMap are efficient for locating a value based on a key and inserting and deleting values based on a key.

2. LinkedHashmap<E>: A doubly linked list implementation.

3. TreeMap<E> : A Red-Black tree based NavigableMap implementation. The map is sorted according to the natural ordering of its keys, or by a Comparator provided at map creation time, depending on which constructor is used.
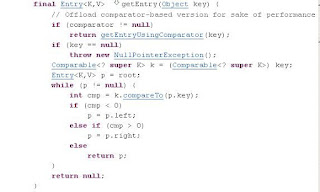
This implementation provides guaranteed log(n) time cost for the containsKey, get, put and remove operations.

TreeMap performs all key comparisons using its compareTo (or compare) method, so two keys that are deemed equal by this method are, from the standpoint of the sorted map, equal. 

 According to the API documentation the Treemap is a red-black tree. Please refer this to understand more.

 

Set<E> Interface. 

A collection that contains no duplicate elements. More formally, sets contain no pair of elements e1 and e2 such that e1.equals(e2), and at most one null element.

1. Great care must be exercised if mutable objects are used as set elements.

Key implementations of Setinterface

1. HashSet <E>: This class implements the Set interface, backed by a hash table (actually a HashMap instance). It makes no guarantees as to the iteration order of the set; in particular, it does not guarantee that the order will remain constant over time. This class permits the null element.

1. Implements all optional set operations, underlying data structure is Hash Map.
2. permits null but only one null value.
3. This class offers constant time performance for the basic operations (add, remove, contains and size), assuming the hash function disperses the elements properly among the buckets
4. Iterating over this set requires time proportional to the sum of the HashSet instance's size (the number of elements) plus the "capacity" of the backing HashMap instance (the number of buckets). Thus, it's very important not to set the initial capacity too high (or the load factor too low) if iteration performance is important.

Key operations algorithm

 
     

2. LinkedHashSet<E>:  A LinkedHashSet is an ordered version of HashSet that
maintains a doubly-linked List across all elements. Use this class instead of HashSet
when you care about the iteration order. When you iterate through a HashSet the
order is unpredictable, while a LinkedHashSet lets you iterate through the elements
in the order in which they were inserted. Does not have any implementation method extend all methods from HashSet<E>

3. TreeSet<E> : A NavigableSet implementation based on a TreeMap. The elements are ordered using their natural ordering, or by a Comparator provided at set creation time, depending on which constructor is used.

This implementation provides guaranteed log(n) time cost for the basic operations (add, remove and contains).

Sorting Algorithms in Java

As the focus on data structures and algorithm increases. The Sorting algorithm are now in more focus esp in Interviews and in other development tasks we do.The purpose of writing this post is to provide information and provide sample code for all the sorting algorithm on one page or redirect on relevant pages. The post will not add anything that is not already available on Internet it will just aggregate the relevant information under one post.

Prior knowledge
One must know basic Java  and the commonly data structures supported in Java.

Basics :

Definitions of all the sorting algorithms and there basic algorithm is given  in this Sorting algorithm page of wiki. These basic definitions of sorting algorithms are sufficient to explain the basic crux of each algorithm.


Sorting algorithms :

1. Bubble sort : Bubble sort is a simple sorting algorithm. The algorithm starts at the beginning of the data set. It compares the first two elements, and if the first is greater than the second, it swaps them. It continues doing this for each pair of adjacent elements to the end of the data set. It then starts again with the first two elements, repeating until no swaps have occurred on the last pass.

•   When to use : 1. In case the list size to be sorted is small  2.In case there only few or one element is not in position.

Coding Example  : Coding example for bubble sort can be found here.

•  This algorithm's average and worst case performance is O(n²), so it is rarely used to sort large, unordered, data sets.

2.Selection Sort :  One of the simplest sorting algorithms works as follows: First, find the smallest item in the array and exchange it with the first entry (itself if the first entry is already the smallest). Then, find the next smallest item and exchange it with the second entry. Continue in this way until the entire array is sorted. This method is called selection sort because it works by repeatedly selecting the smallest remaining item.

•   When to use : 1. In case the list size to be sorted is small  2.In case there only few or one element is not in position. 3. The maximum number of swaps can be n so this sorting is useful in case of expensive swaps. 

 Coding example : The coding example can be found here.

• This algorithm's complexity is O(n²)

Difference between bubble sort and selection sort : Both the sorting algorithm sounds same.But the key difference is that bubble sort compares adjacent elements till list is fully sorted whereas the selection sort finds the smallest item and places it at the first entry.

3. Insertion Sort : The best definition and explanation for insertion sort is here.


  When to use : 1. The insertion sort can be very fast and efficient when used with smaller arrays. 2. The maximum number of swaps can be n so this sorting is useful in case of expensive swaps.3. Efficient for data sets that are partially sorted

Coding example : The  algorithm is here

int j;
for (j=1;j<=n;j++ ){
    int y = data[j];
    for (int i=j-1; i>=0 && y<data[i] ;i--){
      data[i+1]= data[i];
      data[i]= y;
  }
}

Consider an example of array [6,5,7,2].

1. The variable J starts an iteration from position 1 i.e 5 till 2 position 3
2. On each iteration of J we will start comparing the elements with elements at position less than J
3. if the elements is less the positions are swapped.

• This algorithm's worst case complexity is O(n²) and best case [already sorted array]is O(n).

4. Shell Sort : If you study the insertion sort carefully what it does is it start comparison with the adjacent elements i.e the loop iterates with a gap size of 1. The shell sort suggests that instead of comparing adjacent elements and iterating over a loop with gap size of 1 you should iteration loop with a fixed gap size and that gap size should decrease with every loop.

Coding example : The only change in the algorithm from insertion sort is that there will be an higher loop on the insertion sort code and instead of iterating over elements with gap size of 1 you will iterate over element with different gap sizes till the gap size is 1.The code example is here or here

• This algorithm's time complexity depends on the selection of gap sizes

5. Combo Sort : Combo Sort has same relation with bubble sort as Shell sort have with insertion sort. In case of combo sort the elements are sorted using bubble sort algorithm however they are not sorted by comparing adjacent element rather the elements that are at a gap from the element . This gap is decided by a shrink factor [generally 1.3] .

Coding example : The algorithm  is here.

• This algorithm's worst case complexity is O(n²) and best case [already sorted array]is O(n).

6. Merge Sort : Also called as "Divide and conquer algorithm". The animation representation of the algorithm is here.  
Conceptually, a merge sort works as follows

1. Divide the unsorted list into n sublists, each containing 1 element (a list of 1 element is considered sorted).
2. Repeatedly merge sublists to produce new sublists until there is only 1 sublist remaining. This will be the sorted list.

When to use : 1. This algorithm scales well for large lists also. 

Coding example : The coding example can be found here.

• This algorithm's worst case  and best case complexity is O(n log n).

  In Java, the Arrays.sort() methods use merge sort or a tuned quicksort depending on the datatypes and for implementation efficiency switch to insertion sort when fewer than seven array elements are being sorted.


7. Heap Sort : It is variant of Selection sort but accomplish the sort by using a data structure called a heap [a special type of binary tree]. The details for implementation of heap sort are present here and also here . heap sort is not as popular as quick sort algorithm for sorting.

8. Quick Sort : Quicksort is a divide and conquer algorithm which relies on a partition operation: to partition an array an element called a pivot is selected. All elements smaller than the pivot are moved before it and all greater elements are moved after it. This can be done efficiently in linear time and in-place. The lesser and greater sublists are then recursively sorted.

Coding example : The algorithm is here.

• This algorithm's average case and best case complexity is O(n log n). Worst case is O(n²). The choice of pivot can affects the performance of the algorithm. Prefer way of choosing the pivot is middle or the median of the input array.

9. Counting Sort : Counting sort is applicable when each input is known to belong to a particular set, S, of possibilities. The algorithm runs in O(|S| + n) time and O(|S|) memory where n is the length of the input. It works by creating an integer array of size |S| and using the ith bin to count the occurrences of the ith member of S in the input. Each input is then counted by incrementing the value of its corresponding bin. Afterward, the counting array is looped through to arrange all of the inputs in order.

• The problem with counting sort is memory requirement  as we have to make S number of integer arrays and then stores their count values.

10. Bucket Sort : It is a generalization of counting sort. However the bucket sort's basic principal that is divide the element in to buckets opens up the comparison of this Sort with other sorts. If the size of the bucket in your implementation is 1 as in this example this effectively becomes a counting sort. However if the number of buckets are  two then it effectively becomes a quick sort.

Coding example :  The coding examples are here and here